Electric Field on Continuous Charge Distributions
The electric charge is quantized microscopically.
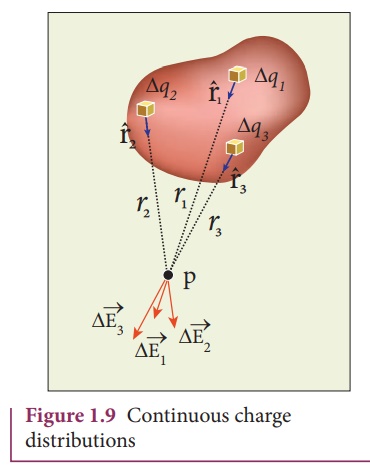
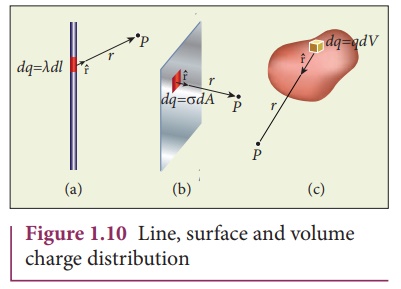
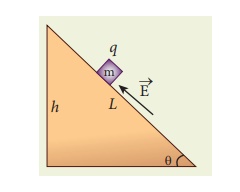
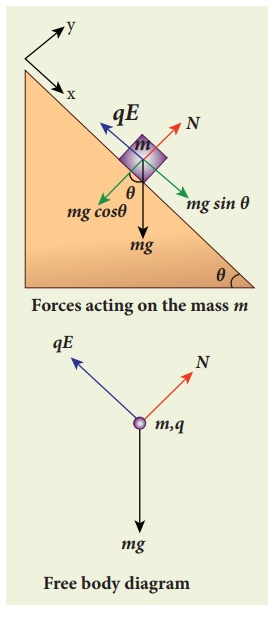
Electric field due to continuous charge distribution The electric charge is quantized microscopically. The expressions (1.2), (1.3), (1.4) are applicable to only point charges. While dealing with the electric field due to a charged sphere or a charged wire etc., it is very difficult to look at individual charges in these charged bodies. Therefore, it is assumed that charge is distributed continuously on the charged bodies and the discrete nature of charges is not considered here. The electric field due to such continuous charge distributions is found by invoking the method of calculus. Consider the following charged object of irregular shape as shown in Figure 1.9. The entire charged object is divided into a large number of charge elements ∆ q 1 , ∆ q 2 , ∆ q 3 ...... ∆ qn and each charge element ∆ q is taken as a point charge. The electric field at a point P due to a charged object is approximately given by the sum of the fields at P due to all such charge elements. Here ∆ qi is the ith charge element, riP is the distance of the point P from the ith charge element and ^riP is the unit vector from ith charge element to the point P. However the equation (1.9) is only an approximation. To incorporate the continuous distribution of charge, we take the limit ∆ q → 0 (= dq ) . In this limit, the summation in the equation (1.9) becomes an integration and takes the following form Here r is the distance of the point P from the infinitesimal charge dq and r is the unit vector from dq to point P. Even though the electric field for a continuous charge distribution is difficult to evaluate, the force experienced by some test charge q in this electric field is still given by (a) If the charge Q is uniformly distributed along the wire of length L, then linear charge density (charge per unit length) is λ = Q/L . Its unit is coulomb per meter (Cm-1). The charge present in the infinitesimal length dl is dq = λdl. This is shown in Figure 1.10 (a). The electric field due to the line of total charge Q is given by (b) If the charge Q is uniformly distributed on a surface of area A, then surface charge density (charge per unit area) is σ = Q/A . Its unit is coulomb per square meter (C m-2). The charge present in the infinitesimal area dA is dq = σ dA. This is shown in the figure 1.10 (b). The electric field due to a of total charge Q is given by This is shown in Figure 1.10(b). (c) If the charge Q is uniformly distributed in a volume V, then volume charge density (charge per unit volume) is given by ρ = Q/V . Its unit is coulomb per cubic meter (C m-3). The charge present in the infinitesimal volume element dV is dq = ρdV. This is shown in Figure 1.10(c). The electric field due to a volume of total charge Q is given by EXAMPLE 1.8 A block of mass m and positive charge q is placed on an insulated frictionless inclined plane as shown in the figure. A uniform electric field E is applied parallel to the inclined surface such that the block is at rest. Calculate the magnitude of the electric field E. Solution Note: A similar problem is solved in XIth Physics volume I, unit 3 section 3.3.2. There are three forces that acts on the mass m: (i) The downward gravitational force exerted by the Earth (mg) (ii) The normal force exerted by the inclined surface (N) (iii) The Coulomb force given by uniform electric field (qE) The free body diagram for the mass m is drawn below. A convenient inertial coordinate system is located in the inclined surface as shown in the figure. The mass m has zero net acceleration both in x and y-direction. Along x-direction, applying Newton's second law, we have Note that the magnitude of the electric field is directly proportional to the mass m and inversely proportional to the charge q. It implies that, if the mass is increased by keeping the charge constant, then a strong electric field is required to stop the object from sliding. If the charge is increased by keeping the mass constant, then a weak electric field is sufficient to stop the mass from sliding down the plane. The electric field also can be expressed in terms of height and the length of the inclined surface of the plane. ![]()
![]()
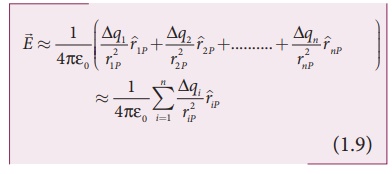
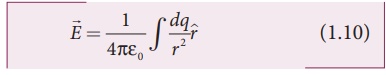
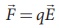 .
. 
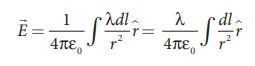
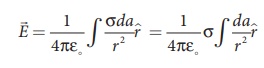
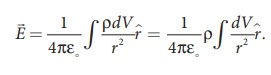
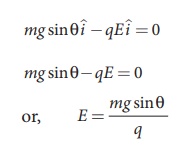
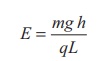
Study Material, Lecturing Notes, Assignment, Reference, Wiki description explanation, brief detail
12th Physics : Electrostatics : Electric field due to continuous charge distribution |
Source: https://www.brainkart.com/article/Electric-field-due-to-continuous-charge-distribution_38362/